ADT(Abstract Data Type)
데이터 구조와 알고리즘을 배우기 전 데이터를 추상적인 수준에서 모델링하는 방법에 대해 설명합니다.
2.1 컨테이너, 관계, 그리고 추상 데이터 타입 (Containers, Relations, and Abstract Data Types)
- 우리는 실세계를 수학적으로 모델링하듯이, 코드를 작성하기 전에 데이터도 추상적인 수준에서 모델링해야 합니다.
- 메모리에 관련된 데이터를 저장, 접근, 조작, 제거해야 하며, 필요한 연산을 공학적으로 분석하고 최소한의 시간과 메모리로 결과를 얻기 위해 설계해야 합니다.
- 데이터의 저장, 접근, 조작, 제거를 모델링하기 위해 **추상 데이터 타입(ADT)**이라는 용어를 사용합니다.
- ADT의 연산은 크게 객체의 속성을 확인하는 **질의(Queries)**와 저장된 객체를 수정하는 **데이터 조작(Data manipulations)**으로 나뉩니다.
2.1.1 컨테이너 ADT (Container ADT)
- 가장 일반적인 ADT는 데이터를 저장하고 접근할 수 있는 객체의 일반적인 모델인 **컨테이너(Container)**입니다.
- 컨테이너에 대한 질의 및 데이터 조작은 일반적인 성격을 가집니다. (예: 생성, 복사, 파괴, 비우기, 삽입, 삭제, 찾기, 크기 확인 등).
2.1.2 단순 및 연관 컨테이너 (Simple and Associative Containers)
- 컨테이너는 객체의 일반적인 모음을 저장하거나, 각 레코드와 연결된 키를 저장할 수 있습니다.
- 객체만 저장하는 컨테이너를 **단순 컨테이너(simple container)**라고 합니다.
- 키를 해당 레코드와 연결하여 저장하는 컨테이너를 **연관 컨테이너(associative container)**라고 합니다 (예: 학생 ID 번호로 학생 기록에 접근하는 Quest 시스템).
- 이 자료에서는 단순 컨테이너에 초점을 맞춥니다. 단순 컨테이너는 연관 컨테이너로 수정될 수 있기 때문입니다.
2.1.3 고유 또는 중복 객체 (Unique or Duplicate Objects)
- 컨테이너는 모든 객체가 고유해야 하거나 중복 객체를 허용하도록 설계될 수 있습니다.
- 중복 객체를 처리하려면 추가적인 코드가 필요하지만, 알고리즘에 대한 추가적인 통찰을 제공하지는 않습니다.
- 따로 언급되지 않는 한, 컨테이너 내의 모든 객체는 고유하다고 가정합니다.
2.1.4 표준 템플릿 라이브러리 (STL) 컨테이너 (Standard Template Library (STL) Containers)
- STL은 객체의 고유성 및 연관성 요구사항에 따라 네 가지 관련 컨테이너를 제공합니다.
- set 예시 코드에서, insert는 중복 값을 무시하며, erase는 해당 값을 제거합니다.
2.1.5 관계 (Relationships)
- 일반적으로 데이터를 저장하는 것 외에 저장된 데이터 사이의 관계도 함께 저장해야 할 수 있습니다 (예: 가계도에서의 가족 관계, 지도에서의 도로 연결).
- 데이터 간에 관계를 저장할 필요가 없는 경우, 해시 테이블이 효율적인 데이터 구조가 될 수 있습니다. 해시 테이블은 객체를 해시 값으로 단순화하고 그 값에 따라 데이터를 구성합니다.
- 그러나 관계에 대해 질문해야 하는 경우가 자주 있습니다.

- 이 자료에서는 선형 순서, 계층적 순서, 부분 순서, 동치 관계, 약한 선형 순서, 인접 관계의 여섯 가지 다른 관계를 다룹니다.
- 이러한 관계는 종종 x = y, x < y, x | y와 같은 부울 값을 반환하는 이항 연산자로 설명되거나, "두 값이 16으로 나눈 나머지가 같은가?"와 같은 부울 값 질문으로 설명됩니다.
- 관계의 속성에는 대칭성(Symmetry), 반대칭성(Anti-symmetry), 그리고 종종 두 관계가 성립할 때 세 번째 관계를 추론할 수 있는 **추이성(Transitivity)**이 있습니다.
2.1.6 관계의 예 (Examples of Relationships)
2.1.6.1 선형 순서 (Linear Orderings)

- x < y, x = y, 또는 y < x 중 하나만 참이고 추이적인 관계입니다. 모든 선형 순서는 반대칭적입니다.
- 객체들은 정렬된(sorted) 시퀀스로 표현될 수 있습니다.
- 예: 정수, 실수, 알파벳, 메모리 위치, 사전식 순서의 단어, 벡터의 사전식 순서.
- 주요 질의 및 연산: 첫 번째/마지막 객체 찾기, k번째 객체 찾기, 객체 삽입/삭제, 객체 정렬 등.
2.1.6.2 계층적 순서 (Hierarchical Orderings)

- x ≺ y는 x가 어떤 면에서 y보다 선행함을 의미합니다.
- 모든 객체에 선행하는 단 하나의 **루트(root)**가 있습니다.
- 임의의 두 객체를 항상 비교할 수 있는 것은 아닙니다.
- 객체들은 목록 대신 트리(tree) 구조로 표현됩니다. 순환이 없습니다.
- 예: 파일 시스템의 디렉토리 구조, Java 및 C#의 상속 계층 구조, 조직 구조, C++ 함수의 변수 범위.
- 속성: 비반사성, 비대칭성, 추이성. 특정 조건에서 공통 후행자를 가진 두 객체 간 순서가 존재할 수 있습니다.
- 주요 질의: 두 객체 중 어느 하나가 다른 하나에 선행하는지 여부 확인, 가장 가까운 공통 선행자 찾기 등.
2.1.6.3 부분 순서 (Partial Orderings)
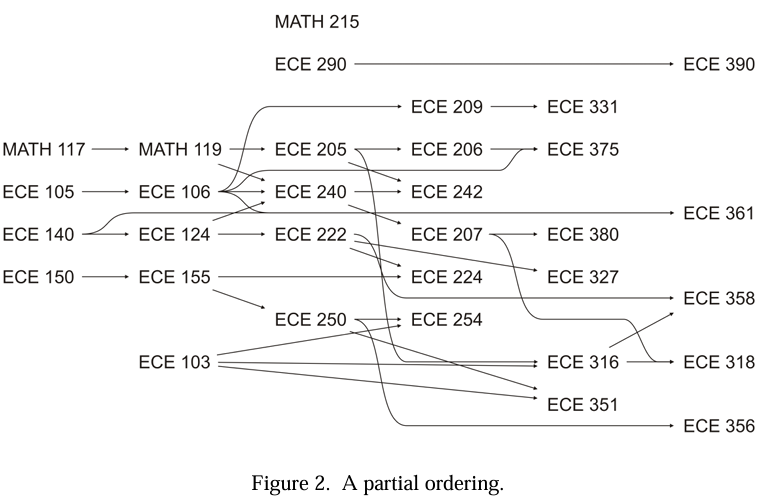
- 계층적 순서보다 제약이 적습니다. x ≺ y는 x가 y보다 먼저 완료되어야 하는 작업(예: 선수 과목)임을 의미할 수 있습니다.
- 흐름은 한 방향으로만 진행되며 순환이 없습니다. 모든 객체가 서로 비교 가능할 필요는 없습니다.
- 예: 다중 상속을 허용하는 C++ 클래스 간의 순서, 작업 의존성(컴파일 종속성 등).
- 속성: 비반사성, 비대칭성, 추이성.
- 계층적 순서와 달리, 두 노드 사이에 여러 경로가 존재할 수 있습니다.

- **격자(Lattices)**는 모든 다른 객체에 선행하는 최하위 요소(⊥)와 모든 다른 객체를 후행하는 최상위 요소(⊤)가 있는 부분 순서입니다.
- 주요 질의: 두 객체 중 하나가 다른 하나에 선행하는지 여부 확인, 선행자/후행자가 없는 객체 찾기, 주어진 객체에 즉시 선행/후행하는 객체 찾기 등.
2.1.6.4 동치 관계 (Equivalence Relations)
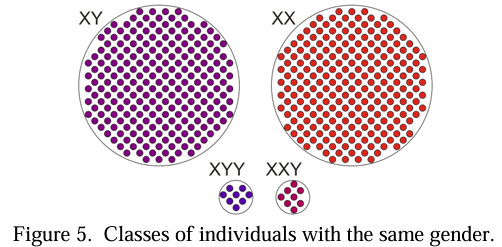
- 두 객체가 관련되어 있거나(동등하거나) 그렇지 않다는 관계입니다.
- 예: 동일한 성별을 가지는 것, 동일한 기능을 가지는 함수 또는 회로.
- 속성: 반사성(x ~ x), 대칭성(x ~ y이면 y ~ x), 추이성(x ~ y이고 y ~ z이면 x ~ z).
- 이러한 속성을 만족하는 관계는 모든 객체를 **동치 클래스(equivalence classes)**로 그룹화할 수 있게 합니다. 클래스 내의 모든 객체는 서로 관련되어 있습니다.
- 주요 질의 및 조작: 두 객체가 동등한지 여부 확인, 특정 동치 클래스에 속하는 객체 수 또는 객체 찾기. 두 동치 클래스를 하나로 병합하는 조작이 가능합니다.
2.1.6.5 약한 선형 순서 (Weak Linear Orderings)

- 동치 클래스들의 선형 순서입니다.
- 예: 나이순으로 사람들을 정렬하는 것 (나이가 같다면 동등).
- STL의 set, multiset, map, multimap 컨테이너는 약한 순서를 사용합니다. set과 map은 동치 클래스당 하나의 객체만 허용하고, multiset과 multimap은 여러 객체를 허용합니다. 동치 클래스 내부 객체의 순서는 보장되지 않습니다.<?>
- 주요 질의 및 조작: 선형 순서 또는 동치 관계에 적용될 수 있는 모든 질의 및 조작이 약한 순서에도 적용될 수 있습니다.
2.1.6.6 인접 관계 (Adjacency Relations)

- 객체 간의 관계가 **그래프(graph)**를 형성합니다. 객체는 정점(vertices), 관계는 **간선(edges)**으로 표현됩니다.
- x ↔ y와 같이 대칭적일 수도 있고 (예: 친구 관계), x → y와 같이 비대칭적일 수도 있습니다 (예: 일방통행 도로).

- 간선에 가중치(예: 거리)를 가질 수도 있습니다.
- 주요 질의 및 조작: 두 정점이 인접한지 여부 확인, 주어진 정점에 인접하거나 연결된 모든 정점 찾기.
- 대칭적인 인접 관계의 **연결된 영역(connected regions)**은 동치 관계를 형성합니다.
- 새로운 관계를 도입하거나 기존 관계를 제거하는 조작이 가능합니다 (예: 도로 건설 또는 폐쇄).
2.1.7 관계 정의 (Defining Relationships)
- 관계는 모든 두 객체를 즉시 비교할 수 있으면 전역적으로(globally) 정의되거나, 쌍별 비교를 통해서만 관계가 정의되는 지역적으로(locally) 정의될 수 있습니다.
- 관계는 객체 자체의 속성에 기반하여 암시적으로(implicitly) 정의되거나, 프로그래머가 관계 집합을 명시적으로 부여하여 명시적으로(explicitly) 정의될 수 있습니다.
- 일반적으로 전역적으로 정의된 관계는 암시적으로 정의되고48, 지역적으로 정의된 관계는 명시적으로 정의됩니다.
2.1.8 추상 데이터 타입 (Abstract Data Types)
- 가장 일반적인 ADT는 컨테이너 ADT입니다. 그러나 실제 데이터는 특정 관계를 가지며, 필요한 질의 및 조작이 제한되는 경우가 많습니다.
- 따라서 특정 관계와 연산을 강조하는 더 구체적인 ADT(예: 정렬된 목록 ADT, 큐 ADT)가 정의됩니다.
- 관계를 저장할 필요가 없는 경우 해시 테이블에 객체를 저장하면 매우 빠르게 질의 및 조작이 가능하지만, 관계를 저장해야 할 때는 더 복잡한 구조가 필요하고 시간과 메모리가 더 많이 소요될 수 있습니다.
- 데이터를 저장, 질의 및 조작할 때는 객체 간의 관계가 무엇인지, 그리고 그 관계에 대해 어떤 질의나 조작이 필요한지를 고려하는 것이 중요합니다.
- 이러한 ADT는 C++ 프로그래밍 언어를 사용하여 알고리즘과 데이터 구조로 구현됩니다.
객체와 컨테이너의 차이
객체와 컨테이너의 차이를 간단히 설명하자면, 객체는 데이터를 포함하고 특정 동작(메서드)을 수행할 수 있는 독립적인 단위이고, 컨테이너는 여러 객체(또는 데이터)를 저장하고 관리하기 위한 자료 구조입니다. 아래에서 자세히 설명합니다.
1. 객체 (Object)
- 정의: 객체는 프로그래밍에서 데이터(속성)와 해당 데이터를 조작하는 동작(메서드)을 하나로 묶은 것입니다. 객체 지향 프로그래밍(OOP)에서 핵심 개념입니다.
- 특징:
예시 (Python):
class Car:
def __init__(self, color):
self.color = color # 속성
def drive(self): # 메서드
print("차가 달립니다.")
my_car = Car("red") # 객체 생성
print(my_car.color) # 출력: red
print(my_car.drive()) # 출력: 차가 달립니다.
2. 컨테이너 (Container)
- 정의: 컨테이너는 여러 객체 또는 데이터를 저장하고 관리하기 위한 자료 구조입니다. 주로 리스트, 배열, 딕셔너리, 집합 등과 같은 형태로 나타납니다.
- 특징:
예시 (Python):
# 리스트(컨테이너)에 여러 객체 저장
cars = [Car("red"), Car("blue"), Car("green")]
for car in cars:
print(car.color) # 출력: red, blue, green
3. 주요 차이점
| 구분 | 객체 | 컨테이너 |
| 역할 | 데이터와 동작(메서드)을 결합한 단위 | 여러 데이터를 저장하고 관리하는 구조 |
| 예시 | Car 클래스의 인스턴스 (my_car) | 리스트 [1, 2, 3], 딕셔너리 {"a": 1} |
| 목적 | 특정 엔터티의 상태와 행동을 표현 | 데이터를 모아 구조적으로 관리 |
| 독립성 | 독립적으로 동작 가능 | 데이터를 담는 틀, 자체 동작은 제한적 |
| 사용 예 | 개별 객체의 속성/메서드 호출 | 여러 객체/데이터를 반복, 검색, 관리 |
요약
- 객체는 데이터와 동작을 가진 독립적인 단위이고, 컨테이너는 여러 객체(또는 데이터)를 모아놓는 저장소입니다.
- 객체는 개별적으로 동작하지만, 컨테이너는 여러 객체를 구조적으로 관리하는 데 초점이 맞춰져 있습니다.
객체지향 설계(OOD) vs. 추상 데이터 타입(ADT)
**객체지향 설계(Object-Oriented Design, OOD)**와 **추상 데이터 타입(Abstract Data Type, ADT)**는 서로 다른 개념이지만, 밀접한 관련이 있습니다. 두 개념은 데이터를 구조화하고 관리하는 방식에 초점을 맞추지만, 접근 방식과 철학에서 차이가 있습니다. 아래에서 차이점과 공통점을 명확히 설명하겠습니다.
1. 추상 데이터 타입 (ADT)
- 정의: ADT는 데이터와 그 데이터에 대해 수행할 수 있는 연산(동작)을 추상적으로 정의한 것입니다. 구현 세부 사항은 숨기고, 사용자에게는 데이터의 인터페이스(어떤 연산을 할 수 있는지)만 제공합니다.
- 특징:
프로그래밍 언어 예시 (Python):
# 스택 ADT의 예
class Stack:
def __init__(self):
self.items = [] # 내부 구현은 리스트
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
여기서 사용자는 push, pop만 알면 되고, 내부가 리스트인지 연결 리스트인지 몰라도 됨.
2. 객체지향 설계 (OOD)
- 정의: 객체지향 설계는 객체 지향 프로그래밍(OOP)의 원칙(캡슐화, 상속, 다형성, 추상화)을 기반으로 시스템을 설계하는 방법론입니다. 객체를 중심으로 데이터와 동작을 결합하여 소프트웨어를 구성합니다.
- 특징:
예시 (Python):
class Car:
def __init__(self, color):
self._color = color # 캡슐화
def drive(self):
print(f"{self._color} 차가 달립니다.")
class SportsCar(Car): # 상속
def drive(self): # 다형성
print(f"{self._color} 스포츠카가 빠르게 달립니다.")
여기서 Car와 SportsCar는 객체 지향적으로 설계된 클래스이며, 상속과 다형성을 활용.
3. 주요 차이점
| 구분 | ADT | OOD |
| 초점 | 데이터와 연산의 추상적 정의 | 객체와 객체 간 상호작용, 시스템 설계 |
| 철학 | 데이터 구조와 인터페이스에 중점 | 현실 세계를 모델링하고 객체 간 관계 강조 |
| 구성 요소 | 데이터 + 연산 | 객체(데이터 + 메서드) + 상속/다형성/캡슐화 |
| 사용 범위 | 주로 자료 구조(스택, 큐 등)에 적용 | 전체 시스템 설계(애플리케이션, 게임 등) |
| 구현 유연성 | 구현 세부 사항을 완전히 숨김 | 구현은 캡슐화되지만, 상속/다형성으로 확장 가능 |
| 예시 | 스택, 큐, 리스트 | 자동차, 은행 계좌, 게임 캐릭터 |
4. 공통점
- 추상화: 둘 다 구현 세부 사항을 숨기고 인터페이스를 제공하는 데 초점을 맞춤.
- 데이터 관리: 데이터와 관련된 연산/메서드를 정의하여 데이터를 구조적으로 다룸.
- 모듈화: 코드의 재사용성과 유지보수를 용이하게 함.
- 예: 스택 ADT는 객체 지향적으로 구현될 수 있으며(클래스로), OOD는 ADT 개념을 포함할 수 있음.
요약
- ADT는 데이터와 연산의 추상적 정의에 중점을 두며, 주로 자료 구조를 다룰 때 사용됩니다.
- OOD는 객체와 객체 간 관계를 중심으로 시스템 전체를 설계하며, 상속, 다형성 같은 OOP 원칙을 활용합니다.
- ADT는 OOD의 일부로 사용될 수 있지만, OOD는 더 포괄적이고 복잡한 시스템 설계를 포함합니다.
용도
추상 데이터 타입(ADT)의 용도는 더 큰 데이터 처리 및 소프트웨어 개발 맥락에서 다음과 같이 논의될 수 있습니다.
- 코드를 작성하기 전의 데이터 모델링 및 추상화: ADT는 메모리에 관련 데이터를 저장, 접근, 조작 및 제거하는 것을 모델링하기 위해 사용되는 용어입니다. 이것은 코드를 작성하기 전에 데이터를 모델링하는 데 사용되는 추상화 수준입니다. 마치 수학을 사용하여 현실 세계 시스템을 모델링하는 것과 유사합니다.
- 효율적인 엔지니어링 분석 및 설계: ADT의 목적은 엔지니어링 분석을 적용하여 수행해야 할 작업을 결정하고, 엔지니어링 설계를 통해 최소한의 시간과 메모리로 결과(데이터 저장 및 조작)를 달성하는 것입니다. 이는 구현 세부 사항(데이터 구조 및 알고리즘)과 분리된 고수준의 설명을 제공합니다.
- 필요한 작업 정의: ADT는 저장된 객체의 속성을 결정하는 **질의(Queries)**와 저장되는 객체를 수정하는 **데이터 조작(Data manipulations)**의 두 가지 일반적인 범주로 나눌 수 있는 작업을 정의합니다.
- 가장 일반적인 데이터 저장소 모델링 (컨테이너 ADT): 가장 일반적인 ADT는 **컨테이너(Container)**입니다. 이는 데이터를 저장하고 접근할 수 있도록 하는 모든 객체의 일반적인 모델이며, 컨테이너에서 수행할 수 있는 질의 및 데이터 조작은 매우 일반적인 성격을 가집니다.
- 데이터 간의 관계 모델링: 데이터를 단순히 저장하는 것뿐만 아니라, 저장된 데이터 간의 관계를 저장해야 할 수도 있습니다. ADT는 이러한 관계(예: 선형 순서, 계층적 순서, 동치 관계, 인접 관계 등) 및 관계에 대한 질의와 조작을 모델링하는 데 사용됩니다.
- 구현 고려 사항과 분리: ADT는 프로그래밍 언어로 구현될 고수준의 설명이며, 적절한 데이터 구조와 알고리즘을 사용하여 구현됩니다. 관계를 저장할 필요가 없는 경우 해시 테이블과 같은 효율적인 데이터 구조가 최적일 수 있지만, 관계를 저장해야 하는 경우 더 복잡한 구조와 더 많은 시간 및 메모리가 필요할 수 있습니다. ADT는 이러한 구현의 세부 사항에서 추상화되어 문제 자체에 집중할 수 있게 합니다.
- 데이터 저장, 질의 및 조작 시 고려해야 할 질문 안내: ADT를 통해 데이터 저장, 질의 및 조작을 수행할 때, 객체 간의 관계, 객체에 대해 수행할 수 있는 질의 및 조작, 컨테이너 전체에 대한 작업, 그리고 관계에 대한 질의 및 조작과 같은 질문을 고려하는 것이 필요합니다.
요약하자면, ADT의 주요 용도는 소프트웨어 개발 초기 단계에서 데이터와 그 데이터를 조작하는 데 필요한 연산 및 데이터 간의 관계를 추상적으로 모델링하여, 이를 통해 효율적인 데이터 구조와 알고리즘 선택 및 설계를 가능하게 하는 것입니다. 이는 구현 세부 사항에 앞서 문제의 핵심 요구 사항을 이해하고 정의하는 데 중요한 역할을 합니다.
데이터 저장, 접근, 조작, 제거
메모리 내 관련 데이터를 다루는 일반적인 작업은 **저장(store), 접근(access), 조작(manipulate), 그리고 제거(remove)**입니다. 이러한 작업들을 수행하는 근본적인 용도는 원하는 결과를 최소한의 시간과 메모리로 달성하는 것입니다. 이를 위해서는 어떤 작업(어떤 제거 작업 등)이 필요한지 결정하는 공학적 분석과 이를 효율적으로 구현하기 위한 공학적 설계가 요구됩니다.
**추상 데이터 타입(ADT, Abstract Data Type)**은 이러한 데이터의 저장, 접근, 조작, 제거라는 용도를 추상적인 수준에서 모델링하기 위해 사용되는 용어입니다.
가장 일반적인 ADT인 **컨테이너(Container)**의 기본적인 용도는 데이터를 저장하고 접근할 수 있도록 하는 것입니다. 컨테이너 ADT는 컨테이너 자체에 대한 일반적인 조작과 더불어, 컨테이너 내부에 있는 객체에 대한 조작도 정의합니다.
- 컨테이너 전체에 대한 용도 관련 질의 및 조작: 컨테이너가 비어있는지 확인하거나, 객체의 개수를 세거나, 새 컨테이너를 생성하거나 복사하고, 컨테이너를 비우는 것과 같은 일반적인 컬렉션 관리 목적.
- 컨테이너 내 객체에 대한 용도 관련 질의 및 조작: 객체를 삽입하고 제거하거나, 특정 객체를 찾거나, 개수를 세거나, 객체들을 순회하는 것과 같은 개별 요소 접근 및 관리 목적.
관계가 필요한 경우, 그 데이터의 용도는 어떤 종류의 관계가 존재하는지, 그리고 그 관계에 대해 어떤 종류의 질의나 조작이 필요한지에 따라 정의됩니다. 출처는 데이터의 용도에 따라 발생할 수 있는 다양한 관계 유형과 그에 따른 질의/조작의 예시를 제시합니다:
- 선형 순서 (Linear ordering): 데이터가 엄격한 순서를 가지는 용도 (예: 숫자 정렬, 사전식 순서). 첫 번째/마지막 찾기, k번째 찾기, 구간 검색, 정렬된 삽입 등의 질의/조작 용도.
- 계층적 순서 (Hierarchical ordering): 데이터가 부모-자식 관계 같은 계층 구조를 가지는 용도 (예: 파일 시스템, 상속 구조). 선행 관계 확인, 공통 선행자 찾기 등의 질의 용도.
- 부분 순서 (Partial ordering): 작업의 선수 과목처럼 완료 순서가 있지만 모든 객체가 서로 비교 가능하지는 않은 용도. 선행/후행 객체 찾기, 선수/후행 작업 확인 등의 질의 용도.
- 동치 관계 (Equivalence relation): 객체들이 특정 기준으로 동등한 그룹으로 묶이는 용도 (예: 같은 성별, 같은 기능의 회로). 동등성 확인, 특정 그룹 찾기, 그룹 병합 등의 질의/조작 용도.
- 약한 선형 순서 (Weak linear ordering): 동치 그룹들이 선형 순서를 가지는 용도 (예: 나이 순서 정렬, 같은 나이는 동등). 선형 순서와 동치 관계에 적용되는 모든 질의/조작 용도. STL의 set, map 등은 이 관계를 사용하며, 고유 객체/키만 저장할지 중복을 허용할지라는 추가적인 용도 고려사항이 있습니다.
- 인접 관계 (Adjacency relation): 객체들이 직접 연결되어 그래프를 이루는 용도 (예: 친구 관계, 도로망). 인접 객체 찾기, 연결성 확인, 관계 추가/제거 등의 질의/조작 용도.
이처럼 데이터의 용도는 단순히 객체를 조작하는 것을 넘어, 객체들이 어떤 특정한 관계를 가지고 있는지 그리고 그 데이터와 관계에 대해 어떤 종류의 질의나 조작이 필요한지에 의해 결정됩니다. 경험적으로, 객체들이 매우 특정한 관계를 가지고 있고 필요한 연산이 제한적이라는 것이 명확해졌기 때문에, 단순히 컨테이너처럼 일반적인 객체 저장소를 넘어 특정한 관계와 연산 요구사항을 반영하는 더 구체적인 ADT (예: 정렬된 리스트 ADT, 대기열 ADT)가 필요하게 되었습니다.
결론적으로, 데이터를 저장, 질의, 조작할 때 가장 중요한 고려사항은 바로 해당 데이터의 용도를 정확히 파악하는 것입니다. 출처는 다음과 같은 질문들을 통해 데이터의 용도를 명확히 할 것을 제안합니다:
- 객체 자체에 어떤 관계가 필요한가?
- 컨테이너 내 객체에 대해 어떤 질의 및 조작이 필요한가?
- 컨테이너 전체에 대해 어떤 연산이 필요한가?
- 객체 간의 관계에 대해 어떤 질의 및 조작이 필요한가?
이러한 질문들에 대한 답, 즉 데이터의 용도에 대한 이해가 곧 적절한 추상 데이터 타입(ADT)을 정의하는 기초가 되며, 이는 궁극적으로 C++와 같은 프로그래밍 언어에서 사용할 최적의 데이터 구조와 알고리즘을 선택하고 구현하는 설계 과정으로 이어집니다.
연산
ADT에서 정의되는 작업(operations)은 크게 두 가지 일반적인 범주로 나뉩니다:
- 질의(Queries): 저장된 객체의 속성을 파악하는 연산.
- 데이터 조작(Data manipulations): 저장된 객체를 수정하는 연산.
질의(Queries)
질의를 데이터 처리를 위해 ADT가 제공하는 핵심 연산 중 하나로 명확히 정의하고 있습니다. 질의는 데이터를 변경하지 않고(non-mutating) 단순히 데이터에 대한 정보를 얻는 연산입니다.
컨테이너 ADT는 컨테이너 자체에 대한 다양한 연산을 정의하며, 여기에는 컨테이너의 상태를 파악하는 질의 연산들이 포함됩니다.
- 컨테이너가 비어있는지 확인하는 empty()
- 컨테이너의 크기를 확인하는 size()
- 최대 용량을 확인하는 max_size() 등
또한, 컨테이너 내부에 있는 개별 객체에 대한 질의 연산도 정의됩니다.
- 특정 객체를 찾아 접근하거나 수정하기 위한 find()
- 특정 객체의 복사본 개수를 파악하는 count()
- 컨테이너 내 객체들을 순회하는 begin()
이러한 질의 연산들은 컨테이너의 용도, 즉 저장된 데이터를 효율적으로 관리하고 필요한 정보를 얻는 데 필수적입니다.
데이터의 용도에 따라 데이터 객체 자체를 저장하는 것을 넘어, 데이터 객체 간의 관계를 저장하고 관리해야 하는지 여부가 중요해집니다. 관계를 저장할 필요가 없을 때는 해시 테이블과 같은 구조가 효과적이며, 이 경우 해시 테이블에 대한 질의 연산 (객체 존재 여부 확인 등)이 빠르게 수행될 수 있습니다. 그러나 관계를 저장해야 하는 경우에는 일반적으로 더 복잡한 데이터 구조가 필요하며, 이 경우 관계에 대한 질의 연산이 중요해집니다.
관계가 필요한 경우, 데이터의 용도는 어떤 종류의 관계가 존재하는지, 그리고 그 관계에 대해 어떤 종류의 질의 연산이 필요한지에 따라 정의됩니다.
데이터 조작(Data Manipulations)
데이터 조작을 데이터를 변경하지 않는 질의와 구별되는, 저장된 객체를 수정하는 연산으로 명확히 정의하고 있으며, 이는 ADT가 제공하는 핵심 연산 중 하나입니다.
컨테이너 ADT는 컨테이너 자체에 대한 다양한 연산을 정의하며, 여기에는 컨테이너의 상태를 변경하는 데이터 조작 연산들이 포함됩니다.
- 새로운 컨테이너를 생성하는 Create
- 기존 컨테이너를 복사하는 Copy
- 컨테이너를 파괴하는 Destroy
- 컨테이너를 비우는 Empty
- 두 컨테이너를 병합하는 Take the union of (or merge)
또한, 컨테이너 내부에 있는 개별 객체에 대한 데이터 조작 연산도 정의됩니다.
- 객체를 컨테이너에 추가하는 Insert
- 컨테이너에서 객체를 제거하는 Remove
- 컨테이너 내 객체를 '접근하거나 수정하는' Access or modify 연산 등
특히 Insert와 Remove는 컨테이너의 내용을 직접적으로 변경하는 대표적인 데이터 조작 연산입니다.
데이터의 용도에 따라 데이터 조작 연산의 복잡성이 달라질 수 있습니다. 예를 들어, 컨테이너가 중복 객체를 허용하는 경우, 중복 객체를 다루기 위해 필요한 데이터 조작은 추가적인 코드를 요구할 수 있습니다.
데이터 객체 자체를 저장하는 것을 넘어, 데이터 객체 간의 관계를 저장하고 관리해야 하는지 여부에 따라서도 필요한 데이터 조작 연산의 종류가 달라집니다.
결론적으로, 데이터 저장의 용도를 파악하는 것은 어떤 연산들, 특히 어떤 종류의 질의와 데이터 조작이 필요한지 명확히 하는 과정입니다. 출처는 필요한 데이터 조작 및 질의의 유형에 따라 적절한 추상 데이터 타입을 정의하고, 이를 효율적으로 구현하기 위한 데이터 구조와 알고리즘을 선택해야 함을 강조합니다. 따라서 데이터 조작은 데이터를 단순히 변경하는 행위를 넘어, 데이터가 어떤 용도로 사용될지에 따라 결정되는 핵심적인 연산 요구사항이며, 데이터 처리 시스템 설계의 필수적인 부분입니다.
관계
저장된 데이터 사이의 관계를 함께 저장해야 하는 경우가 많습니다. 예를 들어, 가계도 데이터베이스는 사람뿐만 아니라 가족 관계를 저장해야 하고, 지도 서비스는 도로뿐만 아니라 도로들이 어떻게 연결되어 있는지를 저장해야 합니다5. 데이터 간의 관계를 저장할 필요가 없는 경우, 해시 테이블이 효율적인 데이터 구조가 될 수 있지만6, 관계에 대해 질문해야 하는 경우가 자주 발생합니다.
관계의 속성
객체 간의 관계를 설명하기 위해 대칭성(Symmetry), 반대칭성(Anti-symmetry), 그리고 **추이성(Transitivity)**이라는 세 가지 주요 속성을 논의합니다. 이러한 속성은 관계를 정의하고 이해하는 데 매우 중요합니다.
1. 대칭성 (Symmetry)
- 어떤 관계 ~가 대칭적이라면, x ~ y일 때 오직 그 때만 y ~ x가 성립합니다.
- 예를 들어, 친구 관계(x와 y는 친구다)는 일반적으로 대칭적입니다. 만약 x가 y의 친구라면, y도 x의 친구입니다.
- 소스에서는 x ~ y와 같은 기호를 대칭적인 관계에 사용하는 경향을 보여줍니다.
2. 반대칭성 (Anti-symmetry)
- 어떤 관계 ≺가 반대칭적이라면, x ≺ y 또는 y ≺ x 중 기껏해야 하나만 참입니다8.
- 두 객체 x와 y가 다르고 관계가 반대칭적일 때, 정확히 하나만 참인 경우 x < y 또는 y < x와 같은 기호를 사용한다고 설명합니다.
- 예를 들어, '보다 작다'(x < y) 관계는 반대칭적입니다. x가 y보다 작다면, y는 x보다 작을 수 없습니다.
- 계층적 순서(x ≺ y는 x가 어떤 면에서 y보다 선행함을 의미) 및 부분 순서(x ≺ y는 x가 y보다 먼저 완료되어야 하는 작업) 또한 비대칭적이라고 설명합니다 (반대칭성과 유사한 개념으로 사용된 것으로 보입니다).
3. 추이성 (Transitivity)
- 관계의 흔한 속성은 추이성입니다. 종종 두 관계가 성립할 때 세 번째 관계를 추론할 수 있는 경우입니다.
- 예시:
4. 반사성 (Reflexivity)
- 관계 ~가 반사적이라는 것은 모든 x에 대해 x ~ x가 성립한다는 것을 의미합니다.
- 즉, 모든 객체는 그 자신과 해당 관계를 맺고 있다는 뜻입니다.
이러한 속성들은 소스에서 설명하는 여섯 가지 다른 관계들(선형 순서, 계층적 순서, 부분 순서, 동치 관계, 약한 순서, 인접 관계)을 특징짓는 데 사용됩니다. 예를 들어, 선형 순서는 추이적이며 반대칭적이고, 동치 관계는 반사성(x ~ x), 대칭성, 추이성을 모두 만족하는 관계입니다. 인접 관계는 대칭적일 수도(x ↔ y) 있고 비대칭적일 수도 있습니다(x → y).
결론적으로, 데이터를 추상적으로 모델링할 때 객체 자체를 저장하는 것 외에 객체 간의 관계가 무엇인지, 그리고 그 관계가 **어떤 속성(대칭성, 반대칭성, 추이성 등)**을 가지는지를 이해하는 것이 중요합니다. 이러한 속성은 해당 관계에 대해 어떤 종류의 질의나 조작이 가능하고 필요한지를 결정하는 데 도움을 주며, 이는 궁극적으로 적절한 추상 데이터 타입을 선택하고 효율적인 데이터 구조와 알고리즘을 설계하는 기초가 됩니다.
관계의 정의
관계는 일반적으로 불리언(Boolean) 값을 반환하는 이항 연산자 또는 불리언 값을 반환하는 질문을 사용하여 설명됩니다. 즉, 특정 두 객체 x와 y에 대해 어떤 관계가 성립하는지 여부를 "참" 또는 "거짓"으로 판단할 수 있다는 것입니다.
출처에서 관계를 설명하기 위해 제시하는 예시는 다음과 같습니다:
- 두 값이 같은가? (x = y)
- 한 값이 다른 값보다 작은가? (x < y)
- 한 값이 다른 값을 나누는가? (x | y)
- 두 값이 모듈러 16에 대해 같은 나머지를 가지는가?
- 두 정수가 최대 하나의 소인수만큼 차이가 나는가?
데이터 간의 관계를 저장할 필요가 없는 경우, 해시 테이블과 같은 데이터 구조가 효율적일 수 있지만, 관계에 대해 질의(Query)해야 하는 경우가 자주 발생하기 때문에 관계 모델링이 중요해집니다.
관계는 정의되는 방식에 따라 다음과 같이 구분될 수 있습니다:
- 전역적으로 정의되는 관계 (Globally Defined Relationships): 어떤 두 객체라도 즉시 관계를 비교할 수 있습니다. 예를 들어, 실수의 선형 순서는 전역적으로 정의됩니다.
- 지역적으로 정의되는 관계 (Locally Defined Relationships): 관계가 쌍별(pair-wise)로 정의됩니다. 예를 들어, 회사 내에서 두 임의의 직원 간의 정확한 관계를 파악하기 어려울 수 있습니다.
- 암시적으로 정의되는 관계 (Implicitly Defined Relationships): 객체 자체의 속성을 기반으로 관계가 정의됩니다. 실수의 선형 순서는 암시적으로 정의됩니다.
- 명시적으로 정의되는 관계 (Explicitly Defined Relationships): 프로그래머가 객체들에게 관계를 직접 부여합니다. 특정 문단의 문자들이 프로그래머에 의해 명시적으로 선형 순서화되는 것이 예시입니다.
일반적으로 전역적으로 정의되는 관계는 암시적으로 정의되고, 지역적으로 정의되는 관계는 명시적으로 정의되는 경향이 있습니다.
'CS (Computer Science) > 자료구조' 카테고리의 다른 글
| 큐(Queue) (1) | 2025.06.08 |
|---|---|
| 스택(Stack) (2) | 2025.06.05 |
| 시간 복잡도 / 공간 복잡도 (0) | 2025.06.04 |
| 연결 리스트(Linked List) (0) | 2025.06.04 |
| 리스트 ADT(추상 데이터 구조 리스트) (1) | 2025.06.04 |
